※ 학습자료 정리한 내용입니다.
[Level 2] 13 데이터 전처리 1_데이터클리닝
13차시 데이터 전처리 1_데이터클리닝
: 데이터를 분석하기 좋은 형태로 만드는 과정
[데이터 전처리의 필요성] **
: 데이터 품질은 분석 결과 품질의 출발점이며, 데이터 품질이 높은 경우에도 데이터 전처리는 필요하다
- 데이터 전처리가 필요한 경우
- 구조적 형태가 분석 목적에 적합하지 않은 경우
- 사용하는 툴, 기법에서 요구하는 데이터 형태가 있는 경우
- 데이터가 너무 많은 경우
- 데이터 품질이 낮은 경우
- 불완전(Incomplete) : 데이터의 필드가 비어있는 경우 "결측치"
- 잡음(Noise) : 데이터에 오류가 포함된 경우 "이상치" ex) 수치형 데이터 중 문자형 존재
- 모순(Inconsistency) : 데이터 간 정합성, 일관성이 결여된 경우 ex) 학점 중 Z 값이 있음
- 전처리된 데이터로 모델을 만들어 패턴, 예측을 찾을 수도 있다
[데이터 전처리의 주요 기법]
- 정제(Cleaning)
- 통합(Integration)
- 축소(Reduction)
- 변환(Transormation)
데이터 정제
[결측값]
- 존재하지 않고 비어 있는 상태
- 후속 분석 결과에 영향이 최소화되도록 데이터를 채울 필요
- 결측값 처리 방법 **
- 수작업으로 채워 넣음
- 특정값 사용
- 평균값 사용 (전체 평균 or 기준 속성 평균) ex) python code
- 가장 가능성이 높은 값 사용 (회귀분석, 보간법 등)
- 해당 데이터 행을 모두 제거
[이상값]
- 이상값으로 판단되는 값에 의해 경향성 훼손 발생
- 탐지 방법
1) 시각화 ( 산점도, Box plot, 히스토그램 등)
2) 수치적 탐지방법 (Box plot - IQR 기준)
3) likelihood : 베이즈 정리에 의해 데이터 세트가 가지는 정상/이상 샘플에 대한 발생확률로 판별
4) kNN : 모든 데이터쌍의 거리를 계산하여 검출
- 처리 방법
1) Tukey
2) Carling
import numpy as np
# 데이터 예시
data = np.array([10, 12, 13, 15, 18, 20, 30, 50])
# 사분위수 계산
Q1 = np.percentile(data, 25)
Q3 = np.percentile(data, 75)
IQR = Q3 - Q1
Med = np.median(data)
# Tukey 방법
tukey_lower = Q1 - 1.5 * IQR
tukey_upper = Q3 + 1.5 * IQR
# Carling 방법
carling_lower = Q1 - 1.5 * (Q3 - Med)
carling_upper = Q3 + 1.5 * (Med - Q1)
print("Tukey 이상값 경계:", tukey_lower, tukey_upper)
print("Carling 이상값 경계:", carling_lower, carling_upper)
Q. 동떨어져 있는 데이터는 항상 이상값인가?
떨어져 있으나 데이터가 여러 개 있으면 이상값이 아니라, 새로운 집단인지 확인 필요
[잡음]
14차시 데이터 전처리 2_통합 및 축소
[결합 Join]
- Excluding join



[축소]
- Filtering: 필요한 데이터만 추출
- Sampling: 데이터의 양을 조절
- 차원 축소..
차원의 저주: 차원이 늘어날수록 데이터분석은 잘 됨
[표본 추출 Sampling]
전수조사 vs 표본조사
- 전수조사는 비용과 시간이 많이 드는 단점이 있음 ex) 인구 센서스
- 전수조사를 하면 당연히 샘플 수가 많기 때문에 현실세계에 가까운 결과가 나오지만, 보통 표본조사로 함
전수검사가 어려운 예
- 파괴실험
- 대통령 후보 지지도 조사
- 농축산물 품질 검증
-> 편향성을 줄이기 위해 무작위 추출을 선호함
연구결과를 왜곡시키는 오차 (Error)
- 표본오차: 일부 표본만 조사하기 때문에 발생되는 오차. 전수조사 시, '0'이 됨
비표본오차 -> 전수조사로도 줄이기 쉽지 않음
- 무응답오차 / 휴먼에러(조사자 오차-표본잘못선정, 데이터 잘못분석/ 면접자 오차-실수, 태만/ 응답자 오차-무성의)
[Sampling 방법] *
- 단순임의추출: 무작위 추출
- 층화추출: 지정한 그룹 별로 지정한 비율만큼의 데이터를 임의로 선택. 모집단의 각 층의 비율만큼 추출.
- 계통추출: 첫 번째 요소는 무작위 선정. 매 k번째 요소를 표본으로 선정
1) 만약, 요소들이 주기성을 띄고 있으면 매우 어긋난 표본이 될 수 있으며 모집단을 전혀 반영하지 못하게 됨
2) 만약, 요소들이 무작위로 되어 있다면 단순임의표본과 같다고 할 수 있음
- 군집추출, 집락추출:
1) 군집 간 동질성, 군집 내 이질성인 경우 사용
2) 장점: 군집을 잘 규정하면 비용 절감/ 모집단의 특성과 비교 가능
3) 단점: 단순임의추출보다 군집을 과대, 과소 평가해서 표본오차를 계산하기가 어려울 수 있음
ex) 백화점 지점별 큰 차이가 없다면( 군집 간 동질성 ), 한 지점을 선택하여 그곳 고객들을 대상으로 추출 **
Q. 표본추출방법 4가지 구분
Q. 층화추출 vs 군집추출
[Training - Test Data Split]
Original Data -> Training Set -> 모델링 (머신러닝 알고리즘) -> 모형평가
-> Test Set : 모델의 성능을 테스트하기 위한 데이터 ->
15차시 데이터 전처리 3_변환
[Pivot]
- Pivot : 행, 열 별 요양된 값으로 정렬해서 분석을 하고자 할 때 사용
- Unpivot: wide form -> long form
[파생변수 생성]
파생변수 - "신규"
- 이미 수집된 변수를 활용해 새로운 변수 생성하는 경우
- 주관적일 수 있으며, 논리적 타당성을 갖추어 개발해야 함 ex) 주 구매 매장, 구매 다양
-> 평균값보다 이상이어야 주 구매 매장이라고 판단할 수 있는 타당성을 갖춰야
요약변수 - "집계"
- 빈도를 카운트한 개념
- 원 데이터를 분석 Needs에 맞게 종합한 변수
- 데이터의 수준을 달리하여 종합하는 경우가 많음 ex) 총 구매 금액, 매장별 방문횟수
| 요약변수 | 파생 변수 |
| 매장 이용 횟수 | 주 구매 매장 |
| 구매 상품 품목 | 구매 상품 다양성 |
Q. O/X문제, 변수 설명
Q. 다음 중 요약 변수가 아닌 것을 고르시오
(1) 총 판매량
(2) 총 판매금액
(3) 매장별 방문횟수
(4) 인기 매장 수 : '인기'의 기준은 주관적이고 논리적 타당성이 필요함
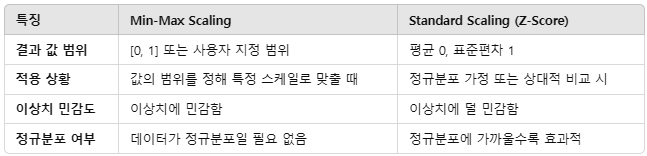
[정규화 Normalization] **
정규화 기법: 데이터 속성값이 ±1.0과 같이 정해진 구간 내에 들도록(표준화) 만들어서 비교 가능하게 만든다.
분포모양은 변하지 않는다.
- 최소-최대 변환 (Min-Max Scaling): 0 ~ 1 사이 값으로 변환.
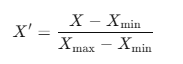
- Z-core 변환 (Standard Z Scaling): 평균이 0, 표준편차가 1로 표준화 값으로 변환. 정규분포이지만 첨도가 다를 수 있는 분포를 비교할 때 사용.
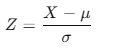
-> 같은 범주 내여야 비교 가능.
-> 변환 전의 데이터가 정규분포를 따를 경우 변환 후는 표준 정규분포를 따를 수 있다.
- Max Absolute Scaling: 가장 큰값의 절대값으로 나눔
- Robust Scaling: 분위수를 이용
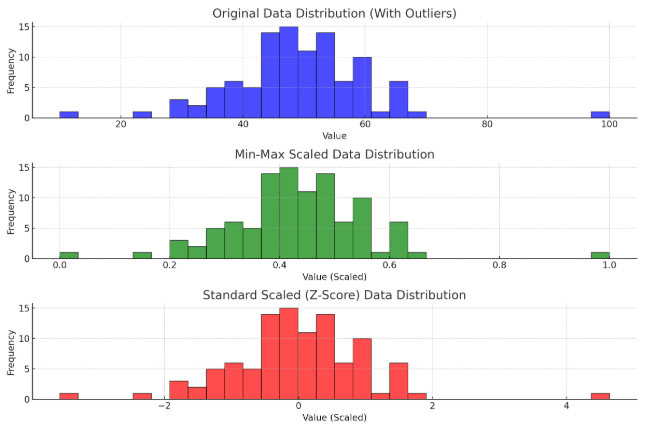
"scaling" : 데이터의 값의 범위를 조정하는 것
Q. 기법 이름 정도 외우기
[데이터 분포의 변환]**
정규분포를 가정하는 분석 기법을 사용하나, 샘플 데이터가 정규를 따르지 않는 경우
정규분포 혹은 가깝게 변환하는 기법
- Positively Skewed (왜도- 오른쪽꼬리) 를 정규분포로 바꿀 때, sqrt(x) -> log10(x) -> 1/x
- Negatively Skewed (왜도- 왼쪽꼬리) 를 정규분포로 바꿀 때,
sqrt(max(x+1)) -> log10( max(x+1)-x ) -> 1/( max(x+1) -x)
Q. Positively skewed 식 외우고, 나머지 하나를 기억하
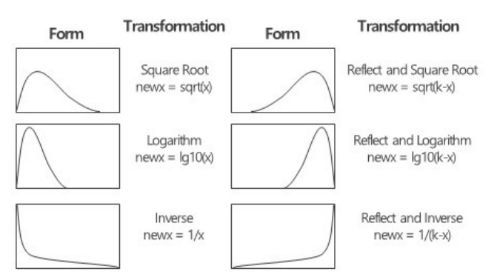
- 종속변수의 증가가 독립변수의 증가보다 급격 -> log 변환 시도 → 큰 값을 축소하여 선형화
- 종속변수의 감소가 독립변수의 증가보다 급격 -> square 변환 시도 → 작은 값을 강조하여 선형화
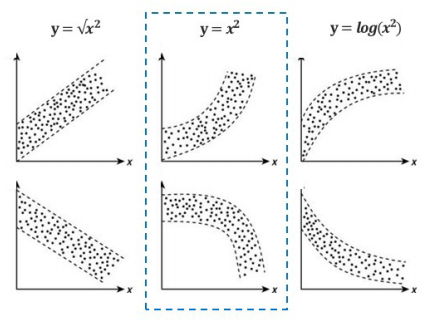
Q. 그림과 함께 문제
'Data Science > 이론' 카테고리의 다른 글
| DS 이론19~20- 선형회귀분석(머신러닝),로지스틱 회귀분석* (0) | 2024.12.03 |
|---|---|
| DS 이론16~18-머신러닝, 특성공학(Under/Over fitting, 모델평가기법) (0) | 2024.12.02 |
| DS 이론 11-선형회귀분석3_이슈처리,성능평가지표,명목형변수 (0) | 2024.11.22 |
| DS 이론10-선형회귀분석2_통계파트(주요 가정) (1) | 2024.11.22 |
| DS 이론09- 선형회귀분석 (0) | 2024.11.20 |