※ 학습자료 정리한 내용입니다.
19차시 선형회귀분석_머신러닝파트
앞에서 배운 통계파트의 선형회귀분석과 접근방식,관심사가 다름. 정확히 딱 분류되어 학습하기!
- 선형회귀분석
1) 독립변수 X로 종속변수Y를 설명할 때, 선형 관계인 경우
2) 독립변수 X가 여러 개일 수 있다
- 선형회귀분석 머신러닝에서는 통계학적 가정(선형성, 정규성, 등분산성, 독립성)이 없음
- 대신, 머신러닝에서도 데이터를 보고 절편, 기울기를 구할 수 있어야 함
선형모델의 핵심은 실제 값($y_i$)과 모델이 예측한 값($\hat{y_i}$)사이의 오차를 최소화하는 것이다.
오차는 MSE(Mean Squared Error) 로 측정한다.
MSE: 실제 값과 예측 값 간의 차이의 제곱의 평균

머신러닝에서는 미분을 통해 MSE의 최소값을 갖는 지점을 찾는 것이 목표
선형회귀 계수의 추정
오차제곱의 합(SSE)이 최소화가 되는 회귀계수들을 어떻게 효과적으로 찾을 수 있을까?

[경사하강법, Gradient Descent]
- 머신러닝에서 오차 함수(또는 비용 함수)를 최소화하는 파라미터를 찾는데 사용되는 최적화 알고리즘
- cost function 이 가장 최소점으로 되어지는 점을 찾음
- cost function은 원래의 값과 가장 오차가 작은 가설함수를 도출하기 위해 사용되는 함
- 일정한 보폭, 혹은 점차 감소하는 보폭으로 이동과 기울기 계산을 반복 -> 원하는 목표지점에 다가올수록 보폭을 줄여야 함

위에 그래프를 보면 x가 음수인 경우에는 그라디언트가 (-) 방향이며, x는 (+) 방향으로 이동하게 됩니다.
반대로 x가 양수라면 그라디언트의 방향은 (+) 이며, x는 (-) 방향으로 이동하게 됩니다
- Learning Rate(보폭)이 크면, 빠르게 수렴하는 대신 발산의 위험이 있고,
작으면 수렴이 너무 느리거나 지역 최저점에서 벗어나지 못할 수 있음
- 임의의 시작점에서 시작하여 다른 지역 최저점에 이를 수 있고, 따라서 단일한 전체 최적을 보장하지는 않음

다중공선성
머신 러닝에서는 크게 상관하지 않음... 통계파트 복습용이라고 생각하시길
[개념]
- 독립변수들 간에 강한 상관관계가 존재하는 상태
- 다중공선성이 있을 때에는 독립,종속 변수 간의 영향 정도를 정확히 산출하지 못하는 현상이 나타남
, 기본적으로 다중공선성 관계를 제거하는데 성능이 좋으면 냅둠
[확인방법]
- X 변수들 간의 산점도나 상관계수를 보아 상관성이 높은지 확인
- VIF (Variance Inflation Factor)가 10 이상인 설명(독립)변수
-> 크면 클 수록 다중공선성이 큼
VIF: 한 설명변수를 Y변수로 하고, 나머지 설명변수를 X변수로 하여 회귀분석을 한 후, 1/ (1-R2)를 구한 값
[해결방법]
- 다중공선성이 있는 독립변수를 제거
- 주성분 분석(PCA)를 통해 추출된 서로 독립인 주성분을 사용하여 회귀분석 수행
- Ridge 나 LASSO 기법을 활용하여 가중치를 조절
PCA: Principal Component Analysis
회귀모형에서 명목형 변수의 처리
[One-Hot Encoding]
- X변수(Column)에 범주형 데이터의 항목을 추가하고 값을 수치( 0, 1) 로 표시
- 단점: 데이터 항목이 다양하면 컬럼 갯수 증가
[Dummy Variable] (or Index Variable) **
- One-Hot Encoding 의 단점인 컬럼이 증가하게 되고 기울기 추정이 불가능해지는 점을 보완
- 1개의 항목을 제거하는 것을 Dummy 화라고 함
Penalized Regression
- Ridge 와 Lasso는 다중공선성을 정규화 시키는 방법
- Ridge: 다중공선성 관계가 있는 독립변수의 가중치를 조절하는 기법. 영향력을 줄임

- Lasso: 다중공선성 관계가 있는 독립변수를 삭제하는 기법

이 둘을 혼합해서 사용하는 것이 엘라스틱?...
2024.12.07 - [Data Science/실습] - DS 실습 13~14- 단순/다중 회귀분석
DS 실습 13~14- 단순/다중 회귀분석
13차시 단순 회귀분석- 독립변수가 하나- 연속형 종속변수와 독립변수 간 선형관계 및 설명력을 확인하는 기법- 종속변수와 독립변수가 각각 하나인 경우의 단순 선형 회귀 모형- 설명력과 더불
sometipsfor.tistory.com
20차시 로지스틱 회귀분석 *
회귀분석하면, target value에 수치형 data가 들어있구나!
로지스틱은 target value가 수치형 data 이긴 하나, 특정 값 예측이 아니라 (이진)분류 문제를 풀어준다.
분류, Classification
- Supervised Learning, 지도학습의 일종
- 입력 데이터에 존재하는 Feature 값들과 label 값의 class 간의 관계를 학습하여
새로 관측된 데이터의 class 를 예측하는 문제, '이진 분류'
- 활용) 이메일 spam 분류, 고객 이탈 방지(남는다 or 떠난다), HR 직원 행동 예측
[Regression vs Classification]
| 독립변수 | 종속변수 target | |
| 기온 (수치) | 판매량 (수치) | Regression |
| 위치, 요일 (범주) | 판매량 (수치) | Regression |
| 판매량 (수치) | 위치 (범주) | Classification |
| 위치, 요일, 기온 (수치 + 범주) | 판매량 200 이상 여부 (범주) | Classification |
로지스틱 회귀, Logistic Regression
! 기본 개념: 최종으로 나오는 y 종속변수는 확률이 들어감
[이진 분류]
- Label 값으로 0/1, Y/N 과 같은 2가지 class만 가능
[프로세스 개요]
- 경사하강법(gradient descent) 로 최적화된 기울기(coefficient) 와 절편(intercept) 을 계산
- threshold 값을 조절하여 positive class 와 negative class를 어떻게 나눌지를 설정
-> y 값을 확률로 가정. 대부분 0.5를 기준으로 하고, 0.5 보다 크면 1 or Y, 작으면 0 or N 으로 분류

종속변수 y가 범주형 데이터(0 or 1)라면, 선형회귀를 따라가면 의미없는 데이터가 많아진다.
이런 경우, 선을 변형시킨 로지스틱 회귀를 따라 변수와 확률 값의 관계가 선형이 아닌 S-커브 형태를 따른다.
회귀식 형태의 모델을 사용하면,
- 각 독립변수의 통계적 유의성을 확인하고, 종속변수에 미치는 영향력 분석 가능
- 일반 선형 회귀에서는 y 예측값 (-∞ , ∞ ) 인 출력 값을
범주형 출력 값을 요구하는 로지스틱 선형 회귀에서는 [0,1] 이 되도록 적절히 변환이 필요

[변환 과정]
1. 수식전개
확률을 만들기 위한 수식 . 시작은 선형회귀 (y= ax+b) 로 시작함!

- 승산비 odds (0~ ∞)
베르누이 시도에서 1이 나올 확률 P와 0이 나올 확률 1− P 의 비율(ratio)을 승산비(odds ratio)
ex) 확률 0.9 = 일어날 가능성 : 일어나지 않을 가능성을 비율로 표현 (90:10) -> 승신비 = 9
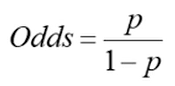
- 로짓함수 log(Odds) (- ∞ ~ ∞)

2. 확률 P 구하기

- 역함수 logistic(x) = P

[Loss Function] **
기울기, 절편 구할 때 사용하는 개념
- Maximize Likelihood
- Minimize Cross-entropy
MSE의 약점은 local minima가 나옴 -> 기울기가 0이 나옴
Cross-entropy 는 한 군데로 Global & Local Minima가 모임

Q. 선형분류 모델(선 하나를 긋는)은 XOR GATE 문제를 절대 풀지 못함. 선 하나로 분류할 수 없음

[Multi Layer Perceptron, MLP]
- 선을 두개 사용하여 XOR 분류할 수 있음
[임계값, Thresholds]
- default 0.5
- P( Y = 1) >= 임계값이면 1로 분류, P(Y = 1) < 임계값 이면 0으로 분류
- 0.5는 절대값이 아니고,
임계값을 조금 낮추면 민감도(Recall)가 높아져 오분류가 높아지더라도 Y=1인 경우를 최대한 분류
- 반대로, 임계값을 높이면 정확(Precision) 이 높아지게 되어 알파 오류를 최소화하는 경향

[Regression 과 비교] **
- 선형 회귀
1) 종속변수는 y값 자체
2) 회귀계수는 해당 독립변수 값이 1단위 증가할 때, 종속변수 y의 변화량
3) 비용함수는 예측오차의 최소화
- 로지스틱 회귀
1) 종속변수는 logit 확률로부터 도출한 class 값
2) 회귀계수는 해당 독립변수 값이 1단위 증가할 때, log (odds) 변화량
3) 비용함수는 cross entropy 의 최소화 or log likelihood의 최대화
[ROC, Receiver Operating Characteristic / AUC, Area Under the Curve]
로지스틱 회귀 평가 방법
- 곡선은 FPR(false positive rate)에 대한 가능한 TPR(True Positive rate)을 표시
- AUC = 1 이면, 분류기가 Positive 와 Negative를 완벽하게 분리
- AUC = 0.5 이면, 분류기가 Positive 와 Negative 를 구분하지 못함( 무작위 임의 선택과 같은 수준)
- AUC 는 면적이 클수록 성능이 좋아짐. fair < 0.8~0.9 good < excellent


Q. TRR, FRR 위치/ 뜻
2024.12.06 - [Data Science/실습] - DS 실습 15- 로지스틱 회귀분석
DS 실습 15- 로지스틱 회귀분석
2024.12.03 - [Data Science/이론] - DS 이론19~20- 선형회귀분석(머신러닝),로지스틱 회귀분석* DS 이론19~20- 선형회귀분석(머신러닝),로지스틱 회귀분석*※ 학습자료 정리한 내용입니다. 19차시 선형회귀
sometipsfor.tistory.com
'Data Science > 이론' 카테고리의 다른 글
| DS 이론 22- 나이브베이즈분류, 예제 (0) | 2024.12.08 |
|---|---|
| DS 이론 21- KNN 알고리즘 (0) | 2024.12.08 |
| DS 이론16~18-머신러닝, 특성공학(Under/Over fitting, 모델평가기법) (0) | 2024.12.02 |
| DS 이론13~15-데이터 전처리(결측치, 정규화, 변환) (1) | 2024.11.23 |
| DS 이론 11-선형회귀분석3_이슈처리,성능평가지표,명목형변수 (0) | 2024.11.22 |