※ 학습자료 정리한 내용입니다.
[이전 내용]
2024.11.20 - [Data Science/이론] - DS 이론09- 선형회귀분석
DS 이론09- 선형회귀분석
※ 학습자료 정리한 내용입니다. - 상관분석을 통하여 두 변수 간에 선형성이 있음을 알았으나, 인과관계를 알 수는 없음! 회귀분석 (Regression Analysis)- (상관분석을 통해서) 두 개의 변수가 선
sometipsfor.tistory.com
선형회귀분석의 4가지 가정 ***

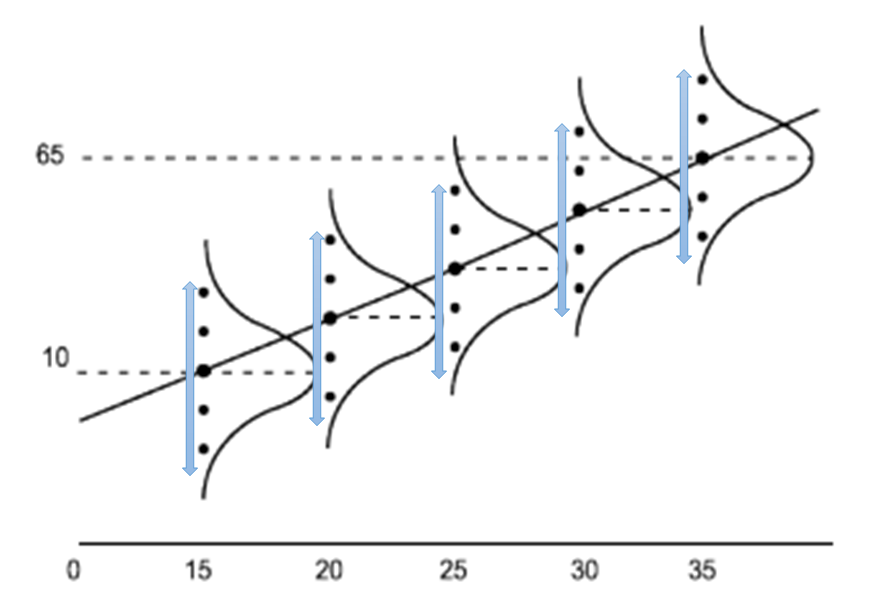
출처: http://kocw-n.xcache.kinxcdn.com/data/keris/2021/leeyoonmo1021/3-4.pdf
- 선형성 : 독립변수와 종속변수 간 선형관계
- 정규성 * : 오차 분산의 형태. 한 개의 x 가 가진 y 값의 오차 분산 형태.
- 등분산성 * : 오차의 퍼짐의 정도가 비슷함. 한 개의 x에 대해 여러 개의 y 값을 가짐
- 독립성 * : 각 오차는 독립성이 있고 동일하게 분포하는 확률분포. 여러 독립변수들 간의 상관관계가 없어야 함 (다중공선성이 없어야 함)
- * 은 오차에서 사용되는 가정
- 가정 사항에 적합한가를 파악하기 위한 오차 분석 필요
Q. 4가지 가정 or 특징이 다른 한 가지는?
잔차와 오차
- 회귀 모형에서 오차를 측정할 수 없기 때문에 오차항의 추정치로서 잔차를 사용
-표본에서 구한 회귀식
\(\hat{y} = \hat{\beta }_0+\hat{\beta}_1x\)
:실제 데이터와 차이가 있음. 잔차 e
-모집단에서 구한 "진짜" 회귀식
\({y} = {\beta }_0+{\beta}_1x\)
:실제 데이터와 차이가 있음. 오차 -> 알 수 없음!
-실제 개념은 동일하게 사용함. 진짜 회귀식은 모르기 때문에 표본 회귀 식으로 사용함
Q. 잔차 와 오차를 설명
잔차: 내가 만든 모델과 실제 관측된 값과의 차이
오차: 진짜 회귀선과의 차이
선형성
- 종속변수 Y 는 독립변수 X에 대하여 선형적인 관계
- 선형성 가정에 대한 검토
- 산점도(Scatter plot)로 선형성 확인
- 상관계수를 계산하여 X와 Y 선형관계 확인
- 회귀계수 \(\beta\) 에 대한 검정
독립성
- 오차는 random 변수. 독립적이며 동일하게 분포하는 확률분포
- 선형 trend 가 보이면 안됨 (경향성을 보이면 안됨)
- 독립성 가정을 깨는 조건(ex.다중공선성) 은 제거하는 것이 맞지만, 무조건은 아님! 성능이 잘 나온다면 제외.
- 독립성 가정이 성립하지 않으면,
- 중요한 설명변수가 누락된 경우 : 회귀분석 모델에 포함되지 않은 독립변수가 실제로 종속변수에 중요한 영향을 미치는 경우. 이 누락된 변수가 오차항과 독립변수 간의 상관관계를 만들어 독립성 가정을 위배
- 회귀식이 적절하지 않은 경우 (ex. 비선형 자료에 대한 선형 회귀 적용)
- 다중공선성 존재 : 입력변수와 연관성이 있음 ex) \({y=\beta_0+\beta_1x_1+\beta_2x_2+\beta_3x_3}\)에서 \({x_3=2x_1}\)인 경우, 연관성이 존재하기 때문에 독립성 가정이 깨짐
- 독립성 가정에 대한 검토
- 예측값 대 잔차 산점도
- 더빈왓슨 테스트 Durbin-Watson test(lag-1 auto-correlation)
- 다중공선성 : 통계학의 회귀분석에서 독립변수들 간에 강한 상관관계가 나타나는 문제이다. 독립변수들간에 정확한 선형관계가 존재하는 완전공선성의 경우와 독립변수들간에 높은 선형관계가 존재하는 다중공선성으로 구분하기도 한다. (출처: 위키백과)
* 상관계수와 다중공선성의 차이로 보는 관점
(1) 선형성 가정에서 상관계수의 의미
- 선형성 가정에서는 독립변수와 종속변수 간의 관계를 평가할 때, 상관계수를 통해 두 변수 간의 선형적 관계가 얼마나 강한지 확인합니다.
- 상관계수가 높다면, 두 변수 간의 선형적 관계가 강하다는 의미이며, 선형회귀를 적용하기에 적합할 가능성이 높습니다.
(2) 독립성 가정에서 다중공선성의 의미
- 다중공선성 문제는 독립변수들끼리 높은 상관관계를 가지는 경우를 말합니다.
- 독립변수들 간의 상관관계가 높으면, 모델이 어떤 독립변수가 종속변수에 영향을 미치는지 명확히 구분하기 어려워집니다. 이는 회귀계수의 신뢰성을 떨어뜨리고 추정 결과를 왜곡시킬 수 있습니다.
- 즉, 독립성 가정에서는 독립변수들 간의 상관관계가 낮아야 모델의 안정성이 보장됩니다.
정규성
- 오차는 모두 평균이 0이고, 분산이 \(\sigma^2\) 인 정규분포
- 회귀식의 오차에 대해서만 요구되는 성질이며, 아주 엄격하게 요구되진 않음

- 정규성 가정이 성립하지 않으면, 선형회귀분석의 가정 검정을 할 수 없음. 실제로 선형관계가 있는 지를 볼때 F검정을 하는데, 분산분석을 할 수 없음 . 카이제곱분포가 분산분석에 대함. 카이제곱분포가 기본 전제조건이 정규성을 갖고 있기 때문에
- 정규성 가정이 성립하지 않으면,
- F-test를 활용한 회귀식에 대한 검정, 예측값에 대한 신뢰구간 검정 등을 신뢰성있게 수행할 수 없음 -> F-test 는 등분산성과 정규성을 기반으로한 검정방법
- 정규성 가정에 대한 검토 **
- 산점도/ 히스토그램/ Q-Q plot (x는 예측, y는 실제값 축 기준으로 45도 각의 선이 형성됨)
- 잔차에 대한 왜도 및 첨도 검토 : Jarque-Bera Testor/and Omnibus Test
등분산성
- 분산 \(\sigma^2\) 은 모든 X에 대하여 일정한 상수임 (종속변수 y의 함수가 아님)
- 등분산성 가정이 성립하지 않으면,
- iid 가정이 성립하지 않음 -> F검정, t검정 사용불가 (왜냐면, 해당 검정 전제 조건에서 배제됨)
- log(y) or sqrt(y)로 변환 -> 데이터를 변환하여 등분산성 가정이 성립될 수 있게 만듦
- 등분산성 가정에 대한 검토
- 예측값 잔차 산점도
- 잔차의 등분산성에 대한 검정 : White test
- Q. 4가지 가정 성립하지 않았을 때의 문제는? 해결 방법은 무엇인 지?
회귀분석의 가정을 만족하지 못할 때
선형성 이슈 (독립변수와 종속변수가 선형 관계가 아닌 경우)
- 확인방법
- 선형성 이슈가 있는 지 산점도 그래프를 그리거나 회귀선을 그려서 확인
- 대응방법 (직선 모양(선형성) 이 나오지 않는다면,)
- 데이터 변환: 입력데이터를 변환시켜서 입력데이터를 선형관계로 만듦
- 다항회귀 (Polynomial Regression)
- 독립변수가 다항으로 구성된 회귀모형
- 독립변수에 지수승을 붙여 여러 항을 결합한 선형회귀식을 구성
- 일반화 가법 모형 (Generalized Additive Model)
- 다른 선형 함수의 결합으로 표현: 입력데이터(독립변수) 형태를 바꿔버림
- ex) \({y=\beta_0+\beta_1x_1+\beta_2x_2}\) .. ▶ \({\hat{y}=\beta_0+f_1(x_1)+f_2(x_2) ... }\)
정규성 이슈 (오차항의 확률분포가 정규분포가 아닌 경우)
- 확인방법
- Q-Q plot으로 확인
- 대응방법
- 데이터 변환
- 일반화 선형 모형 (Generalized Linear Model)
- 종속변수에 변환 함수를 적용 ex) \({y}\) ▶ \({g(\hat{y})}\)
- 이와 같은 함수를 Link Function 이라고 하며, 반응변수의 확률 분포에 따라 사용하는 함수가 정해짐

등분산성 이슈 (오차항의 확률분포가 등분산이 아닌 경우)
- 이상치를 제거하는 것이 중요
- 확인방법
- 잔차 그래프 (잔차: 직접 그린 회귀식과 실제 관측된 y 값의 차이)
- 대응방법
- 데이터 변환
- 가중 선형 회귀 (Weighted Linear Regression)
- 잔차에 가중치를 적용한 제곱값을 최소화하는 기법
- 가중치는 해당 관측치 분산의 역수
- ex) 분산 값이 클수록 point 가 멀어짐 -> 역수 -> 분산 값이 클수록 결과값은 작아짐
- 단점: 관측치 x에 대한 가중치를 계산해야하므로, 연산에 대한 부담이 큼
독립성 이슈 (오차항이 독립이 아닌 경우/ 자기상관성이 있는 경우)
- 확인 방법
- Durbin-Watson 통계량
- 대응 방법
- 자기 회귀모델(Autoregressive Model)
'Data Science > 이론' 카테고리의 다른 글
| DS 이론13~15-데이터 전처리(결측치, 정규화, 변환) (0) | 2024.11.23 |
|---|---|
| DS 이론 11-선형회귀분석3_이슈처리,성능평가지표,명목형변수 (0) | 2024.11.22 |
| DS 이론09- 선형회귀분석 (0) | 2024.11.20 |
| DS 이론07~08-추론통계(점/구간추정),상관분석 (0) | 2024.11.19 |
| DS 이론 06- 연속확률분포(지수,정규,t,카이제곱,f) (0) | 2024.11.18 |