※ 학습자료 정리한 내용입니다.
추론 통계1_추정
Q. 계산 문제. 의미 문제. 많이 나옴
추정, Estimation
: 표본을 통하여 모집단의 특성이 어떠한 가에 대해 추측하는 과정
- 추정량: 표본정보에 의존하는 확률변수로서, 모수를 추정하는 데 사용되는 표본통계량
- 추정치: 추정량을 평가하여 얻게되는 특정한 수치
점추정
- 모집단의 특성을 단일한 값으로 추정하는 방법 (고정된 값)
- 모르는 모수를 가장 잘 대표할 수 있는 표본을 추출하고 필요한 계산을 하여 얻는 하나의 수치
- 표본이 모집단의 특성을 잘 표현하지 못할 경우에는 통계량과 모수 간의 오차가 클 수 있음
- 점추정방법: 적률, 최대우도 -> 표본평균이 모평균의 점추정량이 됨
구간추정 ★
- 모수의 참값이 포함되리라고 기대하는 추정치를 일정한 범위로 나타내는 것
- 모수가 있을 것으로 예상되는 구간과 그 구간에 실제 모수가 있을 예상 확률을 구함
1) 구간 설정: 구간이 좁으면 모수를 좀 더 정확하게 추정하는 것
2) 신뢰도 설정: 설정된 구간에 실제 모수가 존재할 확률
ex) 추정: A사람이 말하길 범인은 서울에, B사람이 말하길 범인은 신촌에
-> 서울보다는 신촌이 범위가 좁으니 좀더 정확하게 추정함
-> 모수를 정확하게 추정 가능
대수의 법칙 ( = 큰 수의 법칙)
- 장기적으로 어떤 사건이 일어날 확률과 그 사건이 일어나는 상대적 빈도 사이의 차이는 궁극적으로 0 에 접근
- 표본 수가 많을수록 통계량의 오차는 0 에 접근
중심극한정리
- 동일한 확률분포를 가진 독립확률 변수 n 개의 평균의 분포는 n이 적당히 크다면 정규분포에 가까워짐
- 원시 데이터의 불규칙성과 그것의 평균값, 원시 데이터의 불규칙성과는 상관없는 평균값 자체의 불규칙성 구별이 필요
구간추정 - 신뢰구간
- 신뢰구간: 모수가 특정확률로 포함될 것이라고 주장하는 범위
- 신뢰구간 추정치: 하한 ≤ 점추정치 ≤ 상한
- 신뢰수준: 모수의 참값이 두 신뢰한계 안에 포함될 것이라고 주장할 때 사용하는 확률
오차율 ★ ★
: 신뢰구간이 모수 μ 을 포함하지 않을 확률을 의미

P(하한 ≤ μ ≤ 상한) = 0.95
→ P(t1 ≤ t ≤ tu) = 0.95
→ t1 ≤ t ≤ tu
→ t1 ≤ t 통계량 ≤ tu

Q. 표본평균 xˉ=50, 표본표준편차 s=10, 표본 크기 n=25인 경우, 95% 신뢰수준의 오차율
50 ± 1.96 * (10/ √25)
-> 모평균의 95% 신뢰구간이라고 추정함
-> 성능이 좋은 것은 구간범위가 좁은 것
t value = 신뢰수준
- 모분산을 모를 때 & n ≥ 30 인 경우 -> 정규분포
: 90% 신뢰수준일 때 1.64
95% 신뢰수준일 때 1.96
99% 신뢰수준일 때 2.57
- 모집단이 정규분포이고 모분산을 모를 때 & n < 30 인 경우 -> t 분포
: 표를 보고 파악
95% 신뢰수준일 때 꼬리부분 확률값 0.025 & 자유도 10 인경우, 2.228
상관분석
: 연속형 두 변수 간의 선형 관계 정도를 검정하는 통계 분석
상관계수, Correlation Coefficient [ -1 , 1 ]
- 산점도를 통한 연관성 파악에 대하여 계량적인 객관성이 필요
- 두 변수 사이의 상관관계의 정도를 나타내는 수치 (선형성이 얼마나 강한 가)
- ± 1에 가까울수록 강한 상관관계를 의미
- 단, 상관계수의 ± 1 에 가까운 경우에도 두 변수 간의 상관관계가 높지 않을 수 있고,
0에 가까운 경우에도 상관관계가 없는 것은 아닐 수 있다 -> 두 변수 간 비선형적 관계
- 상관계수로 기울기는 알 수 없음 (기울기는 인과관계를 의미함-> 회귀분석)
피어슨 상관계수
- 두 변수 간 선형관계의 방향과 강도가 어느정도인지 측정
- ex) 대입시험 접수와 대학 졸업 학점 간의 상관관계

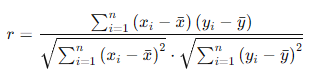
스피어만 상관계수
- 서열척도인 두 변수들의 상관관계를 측정. 변수값들의 순위를 이용함
- ex) 고입시험 등수와 대입시험 등수 간의 관계
켄달 상관계수
- 두 변수를 크기 순으로 두고 순위가 일치하는 정도로 상관계수를 정의
- 두 심사위원이 부여한 등수 간의 관계
'Data Science > 이론' 카테고리의 다른 글
| DS 이론10-선형회귀분석2_통계파트(주요 가정) (1) | 2024.11.22 |
|---|---|
| DS 이론09- 선형회귀분석 (0) | 2024.11.20 |
| DS 이론 06- 연속확률분포(지수,정규,t,카이제곱,f) (0) | 2024.11.18 |
| DS 이론 05- 확률변수, 이산확률분포(베르누이, 이항, 포아송) (1) | 2024.11.17 |
| DS 이론 04- 확률실험, 베이즈정리 (1) | 2024.11.16 |